麦克斯韦方程组有几个_麦克斯韦方程组
1.麦克斯韦方程组微分形式
2.麦克斯韦方程组中, B、 E、 H、 D各代表什么?
3.麦克斯韦方程组的微分形式是什么?
4.什么是"麦式方程组"
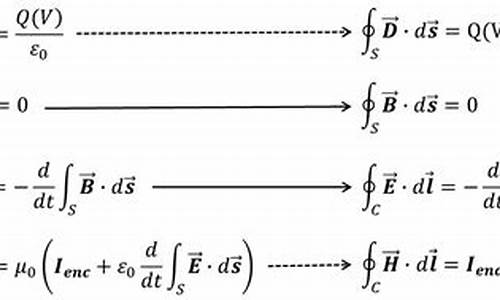
麦克斯韦对法拉第等人和自己的研究工作进行了系统而概括的总结,提出了联系着电荷、电流,、电场、磁场的一个完整的数学方程组。后来,有人对这个方程组又进行了一些加工和整理,成为了电磁场理论的基本方程,人们把它叫做麦克斯韦方程组。由这个方程组得出的结论,大体上有以下几个方面:①不仅变化的磁场能产生电场,而且变化的电场也能产生磁场;②只要有变化的电流,就有变化的电场和变化的磁场在空间的传播,从而形成电磁波;③电磁波中的电场和磁场相互成90度角,而且又都和传播方向相垂直;④电磁波的传播速度始终是一定的,它总是以光的速度传播,1秒中就可以走30万千米。
麦克斯韦方程组微分形式
麦克斯韦方程组的有四种形式,没有八种,如下图所示:
1、描述了电场的性质。在一般情况下,电场可以是自由电荷的电场也可以是变化磁场激发的感应电场,而感应电场是涡旋场,它的电位移线是闭合的,对封闭曲面的通量无贡献。
2、描述了磁场的性质。磁场可以由传导电流激发,也可以由变化电场的位移电流所激发,它们的磁场都是涡旋场,磁感应线都是闭合线,对封闭曲面的通量无贡献。
3、描述了变化的磁场激发电场的规律。
4、描述了传导电流和变化的电场激发磁场的规律。
表面上看,麦克斯韦方程组似乎是超定的(overdetermined)方程组,它只有六个未知量(矢量电场、磁场各拥有三个未知量,电流与电荷不是未知量,而是自由设定并符合电荷守恒的物理量),但却有八个方程(两个高斯定律共有两个方程,法拉第定律与安培定律是矢量式。
各含有三个方程)。这状况与麦克斯韦方程组的某种有限重复性有关。从理论可以推导出,任何满足法拉第定律与安培定律的系统必定满足两个高斯定律。
麦克斯韦方程组中, B、 E、 H、 D各代表什么?
麦克斯韦方程组为:
1、静电场的高斯定理
2、静电场的环流定理
3、磁场的高斯定理
4、安培环路定理
四个方程有积分形式和微分形式,全面的反映了电场和磁场的基本性质,并把电磁场作为一个统一的整体,用统一的观点阐明了电场和磁场之间的联系。因此,麦克斯韦方程组是对电磁场基本规律所作的总结性、统一性的简明而完美的描述。
时变磁场是有旋无散的,磁力线总是闭合的。不闭合的电力线从正电荷到负电荷;闭合的电力线与磁力线相交链;闭合的磁力线要么与电力线交链,要么与电流相交链。
扩展资料:
①几分立的带电体或电流,它们之间的一切电的及磁的作用都是通过它们之间的中间区域传递的,不论中间区域是真空还是实体物质。
②电能或磁能不仅存在于带电体、磁化体或带电流物体中,其大部分分布在周围的电磁场中。
③导体构成的电路若有中断处,电路中的传导电流将由电介质中的位移电流补偿贯通,即全电流连续。且位移电流与其所产生的磁场的关系与传导电流的相同。
④磁通量既无始点又无终点,即不存在磁荷。
百度百科-麦克斯韦方程组
麦克斯韦方程组的微分形式是什么?
D:电位移矢量
B:磁感应强度
H:磁场强度
E:电场强度
其中,B和E是基本量,H和D是辅助矢量。由于历史的原因,误将H称为磁场强度,一直沿用至今。
在麦克斯韦方程组中,E和B是电磁场的基本物理量,它们代表介质中总的宏观电磁场,而D和H只是引进的两个辅助场量.E和D、B和H的关系与电磁场所在物质的性质有关。对于各同性线性物质,它们有如下简单关系:
扩展资料:
一、相关历史
虽然有些历史学家认为麦克斯韦并不是现代麦克斯韦方程组的原创者,在建立分子涡流模型的同时,麦克斯韦的确独自地推导出所有相关的方程。
现代麦克斯韦方程组的四个方程,都可以在麦克斯韦的1861年论文《论物理力线》、1865年论文《电磁场的动力学理论》和于1873年发行的名著《电磁通论》的第二册,第四集,第九章"电磁场的一般方程"里,找到可辨认的形式。
尽管没有任何矢量标记和梯度符号的蛛丝马迹。这本往后物理学生必读的教科书它的发行日期,早于赫维赛德、海因里希·赫兹等等的著作。
二、相关应用
麦克斯韦利用这四个方程计算出了电磁波的传播速度,并发现电磁波的速度与光速相同。于是他预言光的本质是电磁波,后由赫兹由实验证明这一预言的正确性。
从麦克斯韦方程组,可以推论出光波是电磁波。麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。从这些基础方程的相关理论,发展出现代的电力科技与电子科技。
百度百科-麦克斯韦方程
什么是"麦式方程组"
微分形式
在电磁场的实际应用中,经常要知道空间逐点的电磁场量和电荷、电流之间的关系。从数学形式上,就是将麦克斯韦方程组的积分形式化为微分形式。倒三角形为哈密顿算子。
注意:
(1) 在不同的惯性参照系中,麦克斯韦方程组有同样的形式。
(2) 应用麦克斯韦方程组解决实际问题,还要考虑介质对电磁场的影响。例如在均匀各向同性介质中,电磁场量与介质特性量有下列关系:
在非均匀介质中,还要考虑电磁场量在界面上的边值关系。在利用t=0时场量的初值条件,原则上可以求出任一时刻空间任一点的电磁场,即E(x, y, z, t)和B(x, y, z, t)。
下面是高斯单位制下的麦克斯韦方程组
扩展资料
研究背景
他由于列出了表达电磁基本定律的四元方程组而闻名于世。在麦克斯韦以前的许多年间,人们就对电和磁这两个领域进行了广泛的研究,人们都知道这两者是密切相关的。适用于特定场合的各种电磁定律已被发现,但是在麦克斯韦之前却没有形成完整、统一的学说。
麦克斯韦用列出的简短四元方程组(但却非常复杂),就可以准确地描绘出电磁场的特性及其相互作用的关系。这样他就把混乱纷纭的现象归纳成为一种统一完整的学说。麦克斯韦方程在理论和应用科学上都已经广泛应用一个世纪了。
意义
麦克斯韦的主要贡献是建立了麦克斯韦方程组,创立了经典电动力学,并且预言了电磁波的存在,提出了光的电磁说。麦克斯韦是电磁学理论的集大成者。他出生于电磁学理论奠基人法拉第提出电磁感应定理的1831年,后来又与法拉第结成忘年之交,共同构筑了电磁学理论的科学体系。
物理学历史上认为牛顿的经典力学打开了机械时代的大门,而麦克斯韦电磁学理论则为电气时代奠定了基石。
百度百科-麦克斯韦方程组
百度百科-麦克斯韦
麦克斯韦方程组(英语:Maxwell's?equations),是英国物理学家詹姆斯·麦克斯韦在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。它由四个方程组成:描述电荷如何产生电场的高斯定律、论述磁单极子不存在的高斯磁定律、描述电流和时变电场怎样产生磁场的麦克斯韦-安培定律、描述时变磁场如何产生电场的法拉第感应定律。
从麦克斯韦方程组,可以推论出光波是电磁波。麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。从这些基础方程的相关理论,发展出现代的电力科技与电子科技。
麦克斯韦1865年提出的最初形式的方程组由20个等式和20个变量组成。他在1873年尝试用四元数来表达,但未成功。现在所使用的数学形式是奥利弗·赫维赛德和约西亚·吉布斯于1884年以矢量分析的形式重新表达的。
麦克斯韦方程组乃是由四个方程共同组成的:
高斯定律描述电场是怎样由电荷生成。电场线开始于正电荷,终止于负电荷。计算穿过某给定闭曲面的电场线数量,即其电通量,可以得知包含在这闭曲面内的总电荷。更详细地说,这定律描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。
高斯磁定律表明,磁单极子实际上并不存在于宇宙。所以,没有磁荷,磁场线没有初始点,也没有终止点。磁场线会形成循环或延伸至无穷远。换句话说,进入任何区域的磁场线,必需从那区域离开。以术语来说,通过任意闭曲面的磁通量等于零,或者,磁场是一个螺线矢量场。
法拉第感应定律描述含时磁场怎样生成(感应出)电场。电磁感应在这方面是许多发电机的运作原理。例如,一块旋转的条形磁铁会产生含时磁场,这又接下来会生成电场,使得邻近的闭循环因而感应出电流。
麦克斯韦-安培定律阐明,磁场可以用两种方法生成:一种是靠电流(原本的安培定律),另一种是靠含时电场(麦克斯韦修正项)。在电磁学里,麦克斯韦修正项意味着含时电场可以生成磁场,而由于法拉第感应定律,含时磁场又可以生成电场。这样,两个方程在理论上允许自我维持的电磁波传播于空间(更详尽细节,请参阅条目电磁波方程)。
方程组汇览
采用不同的单位制,麦克斯韦方程组的形式会稍微有所改变,大致形式仍旧相同,只是不同的常数会出现在方程内部不同位置。国际单位制是最常使用的单位制,整个工程学领域都采用这种单位制,大多数化学家也都使用这种单位制,大学物理教科书几乎都采用这种单位制。其它常用的单位制有高斯单位制、洛伦兹-赫维赛德单位制(Lorentz-Heaviside?units)和普朗克单位制。由厘米-克-秒制衍生的高斯单位制,比较适合于教学用途,能够使得方程看起来更简单、更易懂。稍后会详细阐述高斯单位制。洛伦兹-赫维赛德单位制也是衍生于厘米-克-秒制,主要用于粒子物理学;普朗克单位制是一种自然单位制,其单位都是根据大自然的性质定义,不是由人为设定。普朗克单位制是研究理论物理学非常有用的工具,能够给出很大的启示。在本段落里,所有方程都采用国际单位制。
这里展示出麦克斯韦方程组的两种等价表述。第一种表述将自由电荷和束缚电荷总和为高斯定律所需要的总电荷,又将自由电流、束缚电流和电极化电流总合为麦克斯韦-安培定律内的总电流。这种表述采用比较基础、微观的观点。这种表述可以应用于计算在真空里有限源电荷与源电流所产生的电场与磁场。但是,对于物质内部超多的电子与原子核,实际而言,无法一一纳入计算。事实上,经典电磁学也不需要这么精确的答案。
第二种表述以自由电荷和自由电流为源头,而不直接计算出现于介电质的束缚电荷和出现于磁化物质的束缚电流和电极化电流所给出的贡献。由于在一般实际状况,能够直接控制的参数是自由电荷和自由电流,而束缚电荷、束缚电流和电极化电流是物质经过极化后产生的现象,采用这种表述会使得在介电质或磁化物质内各种物理计算更加简易。
需要注意的是:麦克斯韦方程组中有B、E两个矢量未知量,共6个未知分量;方程个数是8个(散度是标量,所以两个高斯定律是两个方程;旋度是矢量,法拉第电磁感应定律和安培定律是6个方程;加起来共8个方程),两者并不相等。
麦克斯韦方程组通常应用于各种场的“巨观平均”。当尺度缩小至微观(microscopic?scale),以至于接近单独原子大小的时侯,这些场的局部波动差异将变得无法忽略,量子现象也会开始出现。只有在巨观平均的前提下,物理量像物质的电容率和磁导率才会得到有意义的定义值。
最重的原子核的半径大约为7飞米(7×?10^(?15)米)。所以,在经典电磁学里,微观尺度指的是尺寸的数量级大于10^(?14)米。满足微观尺度,电子和原子核可以视为点电荷,微观麦克斯韦方程组成立;否则,必需将原子核内部的电荷分布纳入考量。在微观尺度计算出来的电场与磁场仍旧变化相当剧烈,空间变化的距离数量级小于10^(?10)米,时间变化的周期数量级在10^(?17)至10^(?13)秒之间。因此,从微观麦克斯韦方程组,必需经过经典平均运算,才能得到平滑、连续、缓慢变化的巨观电场与巨观磁场。巨观尺度的最低极限为10^(?8)米。这意味着电磁波的反射与折射行为可以用巨观麦克斯韦方程组来描述。以这最低极限为边长,体积为10^(?24)立方米的立方体大约含有106个原子核和电子。这么多原子核和电子的物理行为,经过经典平均运算,足以平缓任何剧烈的涨落。根据可靠文献记载,经典平均运算只需要在空间作平均运算,不需要在时间作平均运算,也不需要考虑到原子的量子效应。
最早出现的麦克斯韦方程和其相关理论是为巨观物质设计的,是一种现象学。在那时候,物理学者并不清楚造成电磁现象的基本原因。后来,按照物质的粒子绘景,才推导出微观麦克斯韦方程。二十世纪前半期,在量子力学、相对论、与粒子物理学领域的突破与发展,其崭新理论与微观麦克斯韦方程组相结合,成为建立量子电动力学的关键基石。这是物理学中最准确的理论,所计算出的结果能够精确地符合实验数据。
- 上一篇:北京冬奥奖牌榜排序,北京冬奥奖牌榜排序图
- 下一篇:荷兰队阵容分析最新_荷兰队 阵容